How to Trust Strangers
Composing Byzantine quorum systems for securing distributed protocols
Trust is the basis of any distributed, fault-tolerant, or secure system. We consider systems, such as blockchain networks, that consist of multiple nodes or processes, of which some may fail. A trust assumption specifies the failures that a system can tolerate and determines the conditions under which it operates correctly. In systems subject to arbitrary malicious behavior, or Byzantine faults, the trust assumption is usually specified through sets of processes that may fail together. In the simplest case, this is just the belief that only F nodes among N would fail, where F < N/3. Equivalently, the blockchain networks of proof-of-stake cryptocurrencies assume that misbehavior of participating nodes owning strictly less than third of the stake is tolerated. Tendermint Core, Diem Byzantine Fault Tolerance (DiemBFT), Algorand, Cardano, and many others use this notion of trust. The trust assumption can be generalized and may be symmetric or asymmetric; the latter means that the beliefs of the nodes are subjective, and may differ between nodes.
What should be done when two groups of nodes, each one with their own beliefs, wish to be merged? This post explores how trust assumptions can be composed in symmetric and asymmetric trust models.
Secure distributed systems rely on trust
Technically, trust is defined through a fail-prone system, which is a collection of subsets of processes, called fail-prone sets, such that each of them contains all the processes that may at most fail together during a protocol execution. In order to be well-defined, the fail-prone system needs to satisfy a condition, called the Q3-condition: no three fail-prone sets may cover the whole set of processes the BQS is defined on. Finally, a Byzantine quorum system (BQS) complements the fail-prone system; it indicates the subsets of processes that are self-sufficient in taking important steps during the protocol execution. In the simplest case, the quorums are the complement of the fail-prone sets.
Over the recent years new approaches to modelling trust have been explored. In open, decentralized or permissionless settings, like those of cryptocurrencies running over the Internet, no common trust model may be imposed (or one would have to reintroduce a centralized entity). Instead, every node in the system should be free to choose who to trust and who not to trust. The asymmetric model of trust captures this and forms a natural and necessary extension of the symmetric model.
Concretely, Cachin and Tackmann extend Byzantine quorum systems by introducing the model of asymmetric trust. Each party is now allowed to specify their own fail-prone system, and the set of all these fail-prone systems is called an asymmetric fail-prone system. As in the symmetric case, the notion of quorums exists here as well: each party defines a Byzantine quorum system, and the set of all these forms an asymmetric Byzantine quorum systems (ABQS). Finally, a similar condition as in the symmetric case exists here as well. We will not go into much detail here, but it is called the B3-condition and demands that, for any pair of parties, a certain combination of three of their fail-prone sets do not cover the set of all processes. Equivalently, you can think of this as follows: two processes must have sufficiently many common friends, so they can communicate through them, even if their enemies try to sabotage them.
Composing trust assumptions
In recent work, which will be published at the SRDS 2021 conference, we study how trust assumptions can be composed, when they are expressed through symmetric and asymmetric Byzantine quorum systems. We introduce methods for combining and assembling the trust models of different, possibly disjoint, systems to a common model. Our results provide a key step towards understanding the dynamic evolution of distributed systems and blockchain networks that rely on quorums for resilience.
Composition of symmetric BQS
We first explore the composition of two groups of processes, where each forms a BQS, as a means to allow them to run a protocol jointly, without requiring the members of one group to make assumptions about members of the other group. This is useful in practice because remodeling trust from scratch would be a tedious and subjective process, where nodes in one group would first have to obtain knowledge about the nodes in the other group. We note here that this notion of composition does not consider increasing the resilience for the combined system (which is, of course, a natural avenue for future exploration of the problem); we instead want to put the two BQS next to each other and find a deterministic composition rule that always leads to a new BQS.
Let us start with an example. In the following diagram we show two symmetric BQS. The processes (shown in circles) in the first one are P1 = {a, b, c, d, e} and in the second P2 = {d, e, f, g, h}. Notice that processes d and e are common. The fail-prone systems are F1 = { {a}, {b,c}, {c,e}, {d} } and F2 = { {d}, {e}, {f,g}, {h} }, respectively.
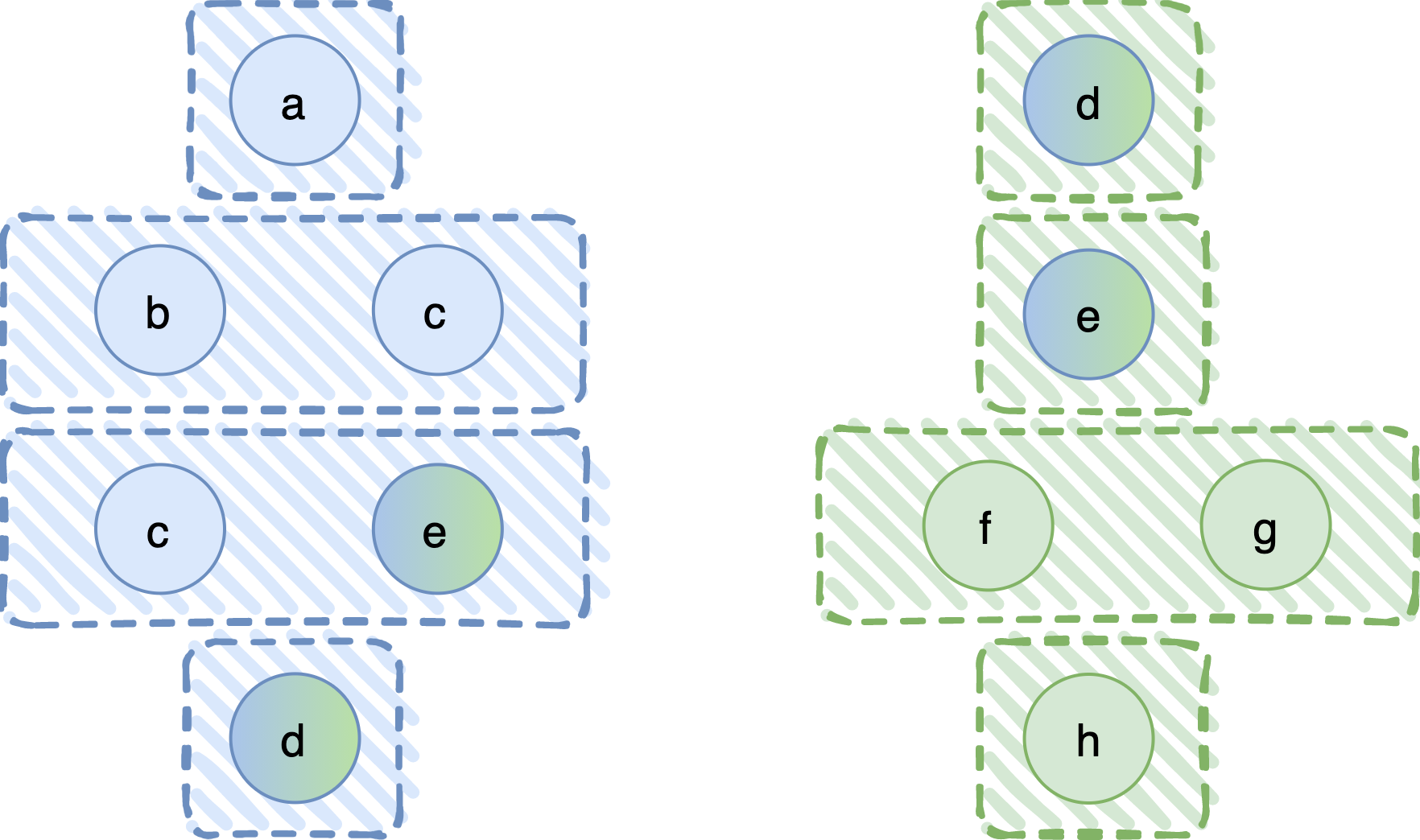
We want to come up with a new, composite BQS, defined on P3 = {a, b, c, d, e, f, g, h}, where processes in some sense retain their trust assumptions, that is, they are not required to make new assumptions on the set P3. So, how do we do that?
A first approach: Union composition
A first thought would be to define the new, composite fail-prone system as the union of the two original ones. This would give F3 = { {a}, {b,c}, {c,e}, {d}, {f,g}, {h} }, also shown in the following figure. Observe that in a fail-prone system we do not keep sets that are subsets of other fail-prone sets, so {e}, for example, does not appear in F3.
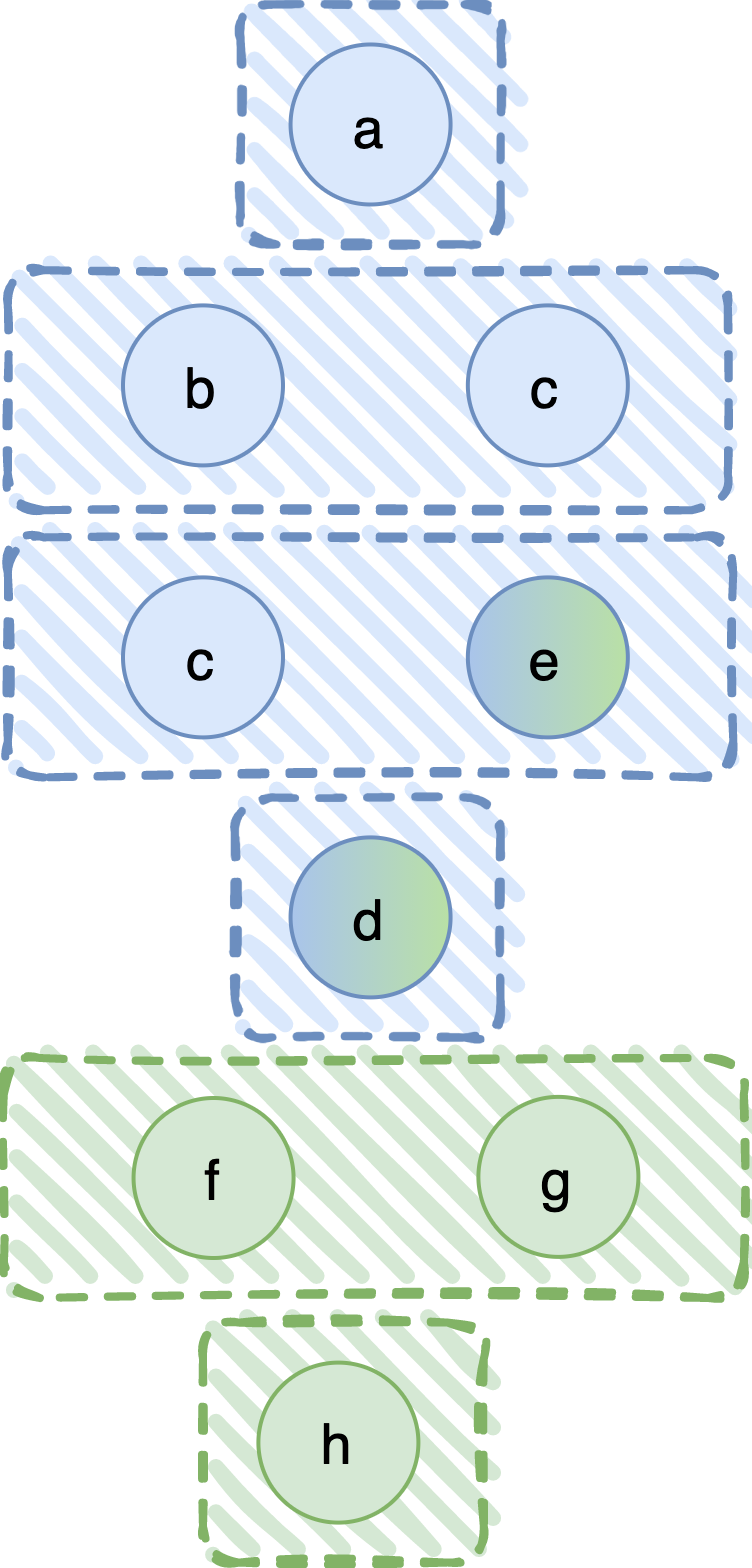
It is true that this rule works, in the sense that it always leads to a BQS (technically, this should be read as “the Q3-condition always holds in the composite system, given that it holds in the original ones”), and processes in one system do not have to come up with new assumptions on the processes on the other. However, the fail-prone sets (and, thus, the tolerated failures in any execution) are rather limited; namely, no combined failure of processes in P1 and P2 is tolerated. Can we do better?
A second approach: Cartesian composition
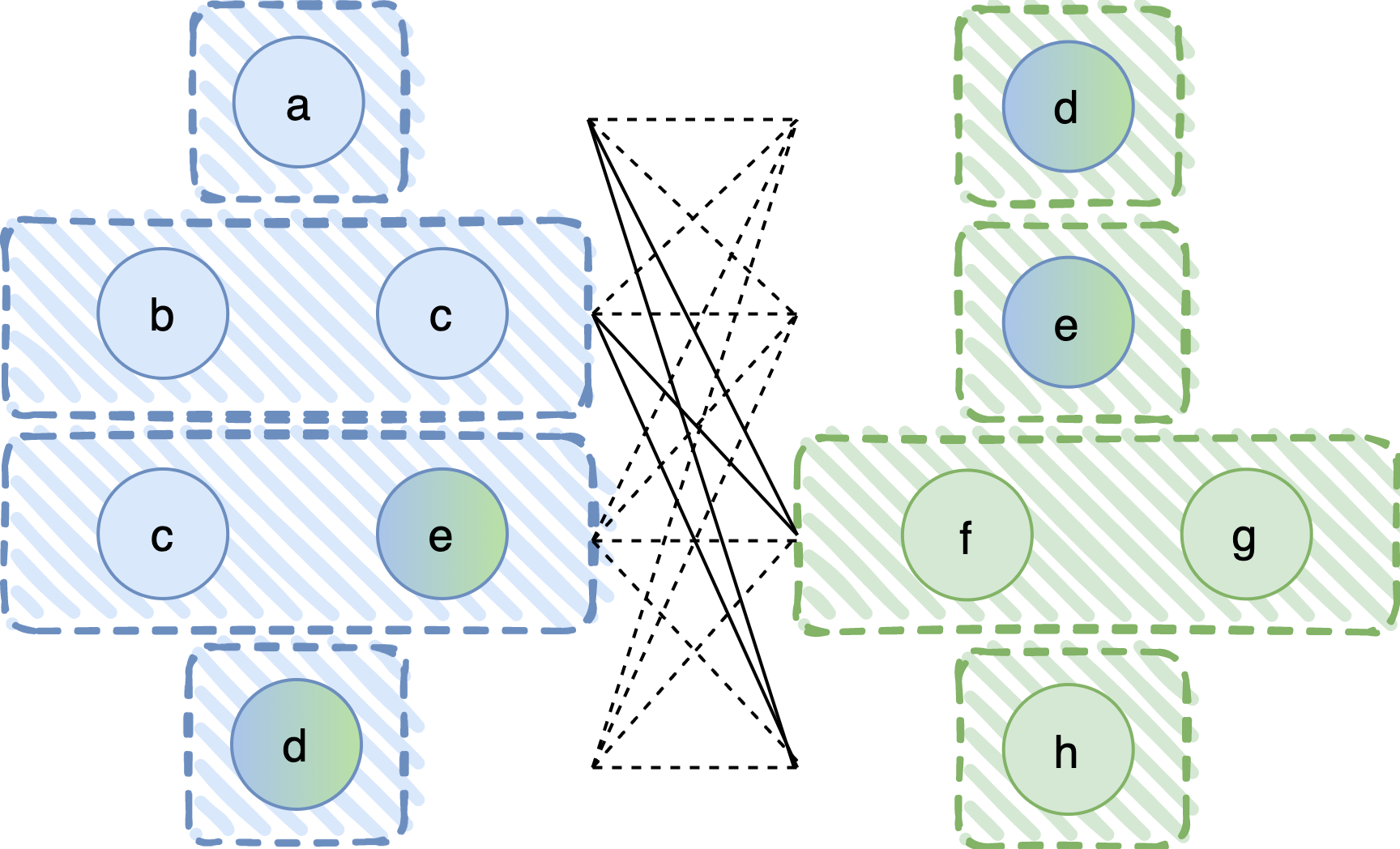
It turns out that we can overcome this limitation. Let us now construct the composite fail-prone system by taking the pairwise union of all fail-prone sets in the first and all fail-prone sets in the second system. Graphically, this could be shown as in the following graph, where the black lines represent set union.
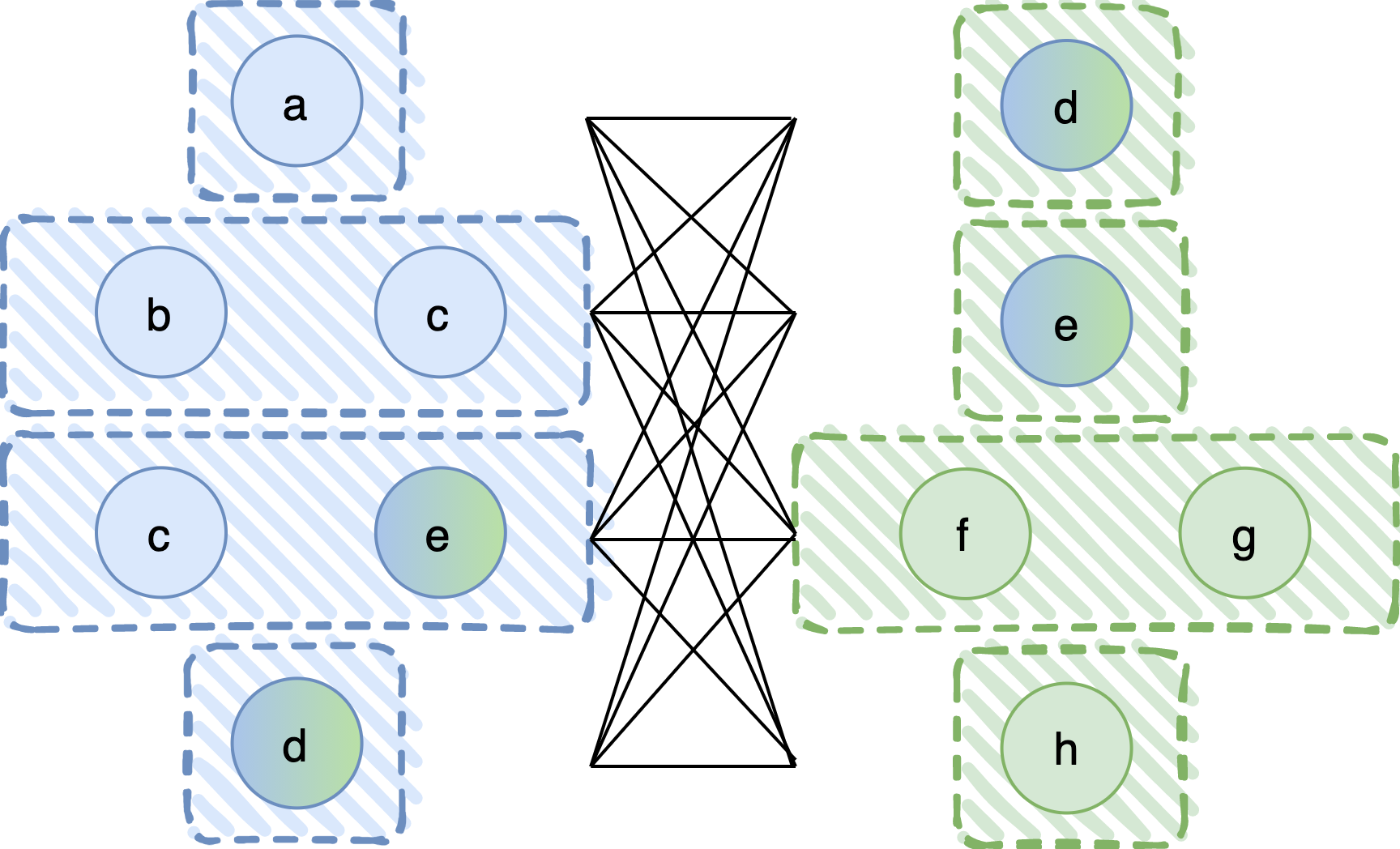
Although this rule explores the right direction, there does exist a problem. Observe that F3, the composite fail-prone system, contains, among others, the sets {a, f, g}, {b, c, h}, and {c, e, d}, also shown in the following figure.
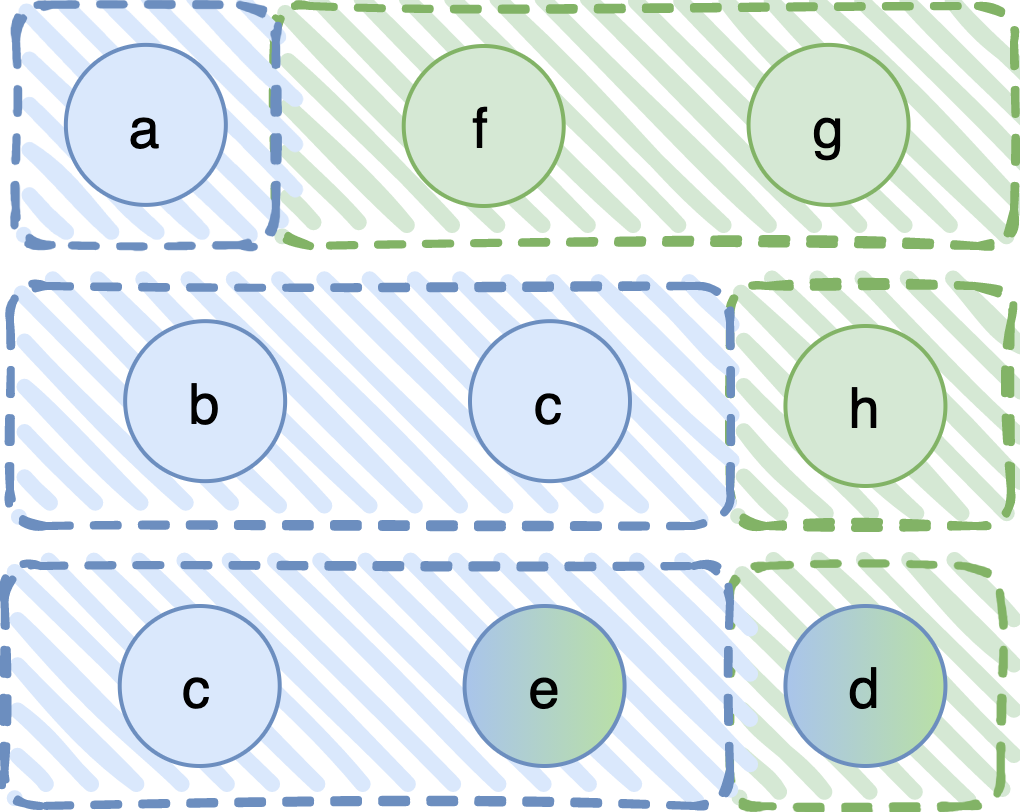
The problem with these three fail-prone sets is that their union covers P3. Hence, the Q3-condition does not hold and we do not have a BQS! But we started from two fail-prone systems that satisfied the Q3-condition, so, why did this happen? The problem is with the last of these sets, {c, e, d}. This set appears in F3, but not in the original systems: its projection in P1, which is {c, e, d}, is not in F1; and its projection in P2, which is {e, d}, is not in F2. In other words, the Q3-condition in the original systems holds because this set is not there. We have created a new fail-prone set that was not considered in the original systems. As a side note, this rule does indeed work (i.e., leads to a system where the Q3-condition holds) if the original systems do not contain common processes.
The final composition rule: Cartesian composition with common processes
So, let us present the composition rule that we discovered and solves the aforementioned problem. We again apply the pairwise union rule, but this time special care is taken when the two sets to be “unioned” contain common processes. Specifically, we union only fail-prone sets that contain exactly the same subset of the processes in common between P1 and P2. In the following figure, this special case is marked by a dashed line.
This results in a fail-prone system F3 as shown in the next figure.
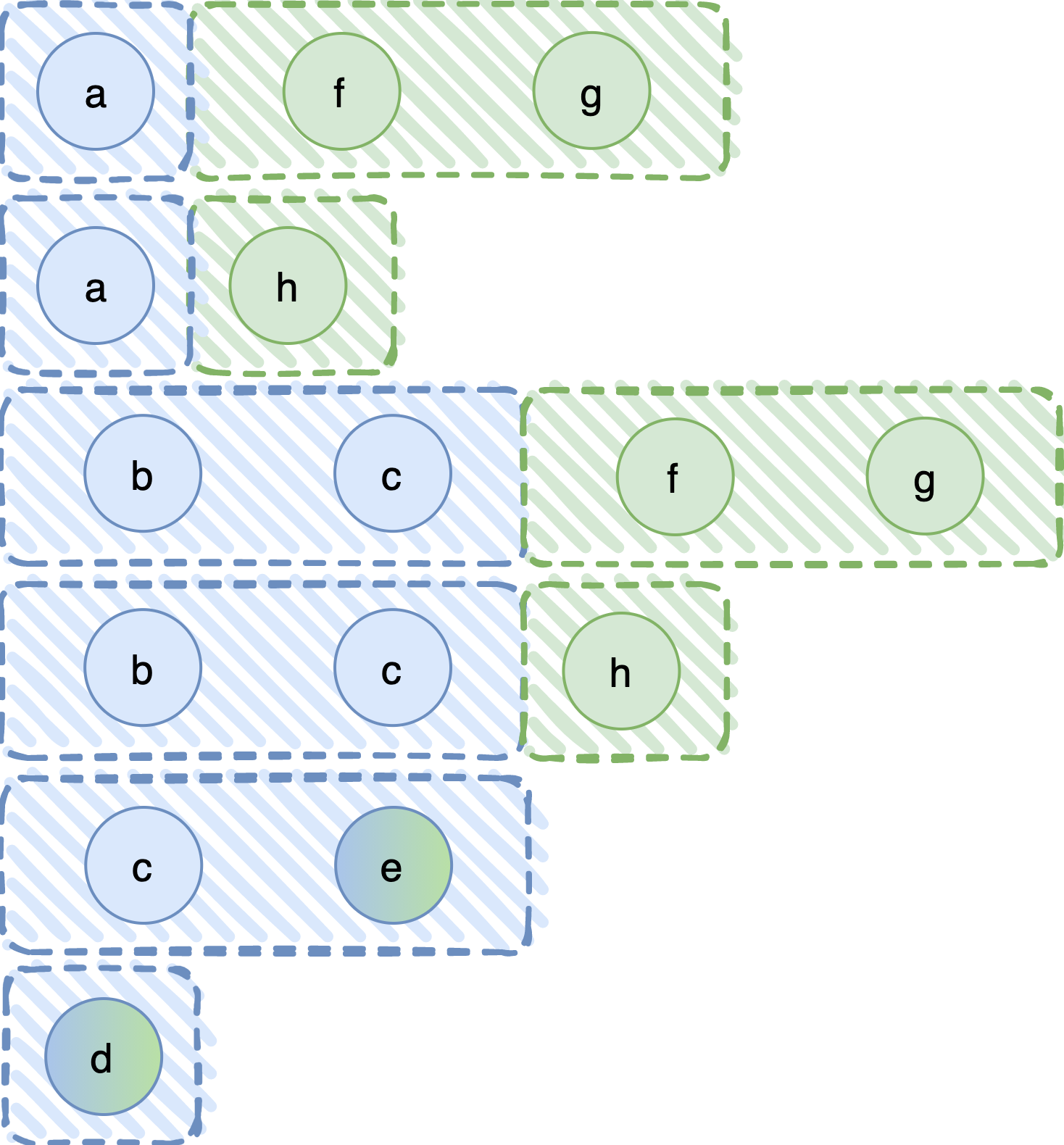
The intuition is that, if some processes in P1, in our case c and e, are Byzantine, then they are Byzantine in P2 as well. They are the same processes after all. Thus, we can join the set {c, e} only with fail-prone sets in P2 that already expect e to fail (in our case there happens to be only one, the fail-prone set {e}).
Composition of asymmetric BQS
An asymmetric Byzantine quorum system (ABQS) is notoriously hard to define. As we explained, the processes are allowed to choose their fail-prone and quorum systems, or, somewhat informally, their friends and enemies. However, the fail-prone and quorum systems have to satisfy certain intersection conditions; as we have seen, two processes must have sufficiently many common friends, so they can communicate through them, even if their enemies try to sabotage them.
Hence, a deterministic rule to compose two ABQS is required, one that guarantees that the intersection properties will always hold in the composed system, given that they hold in the original ones. Such a rule would allow two groups of “strangers” to work together, without requiring a process in one group to make new assumptions on the processes in the other.
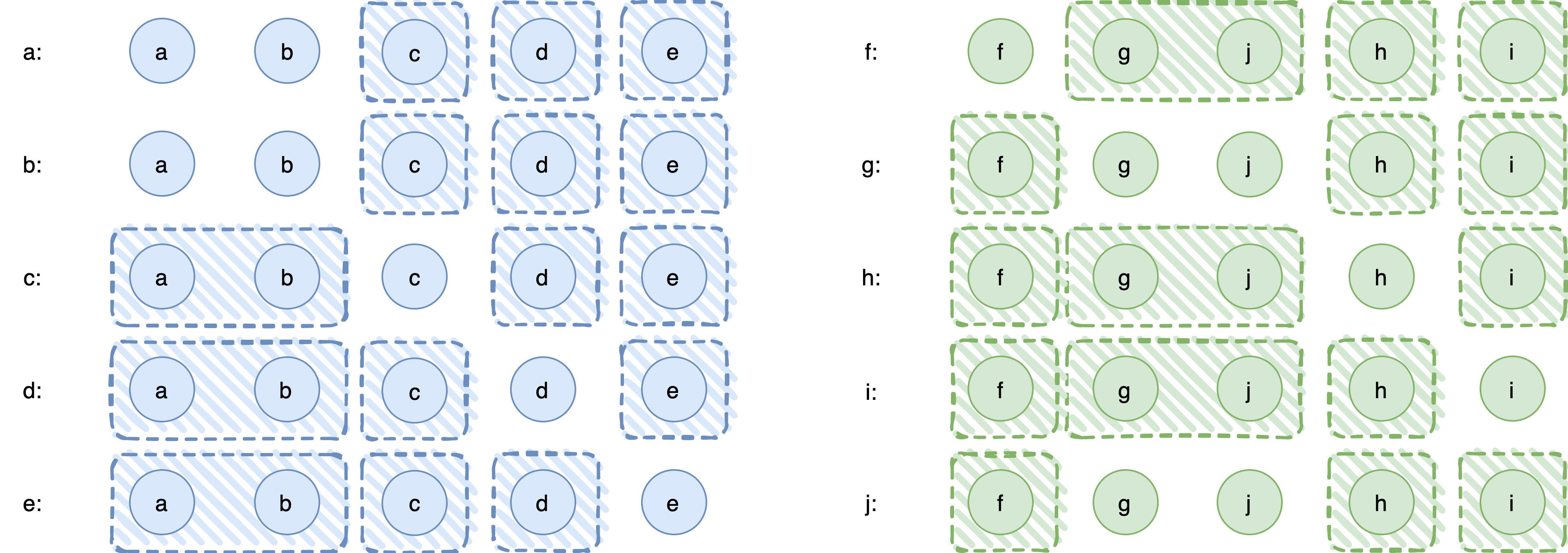
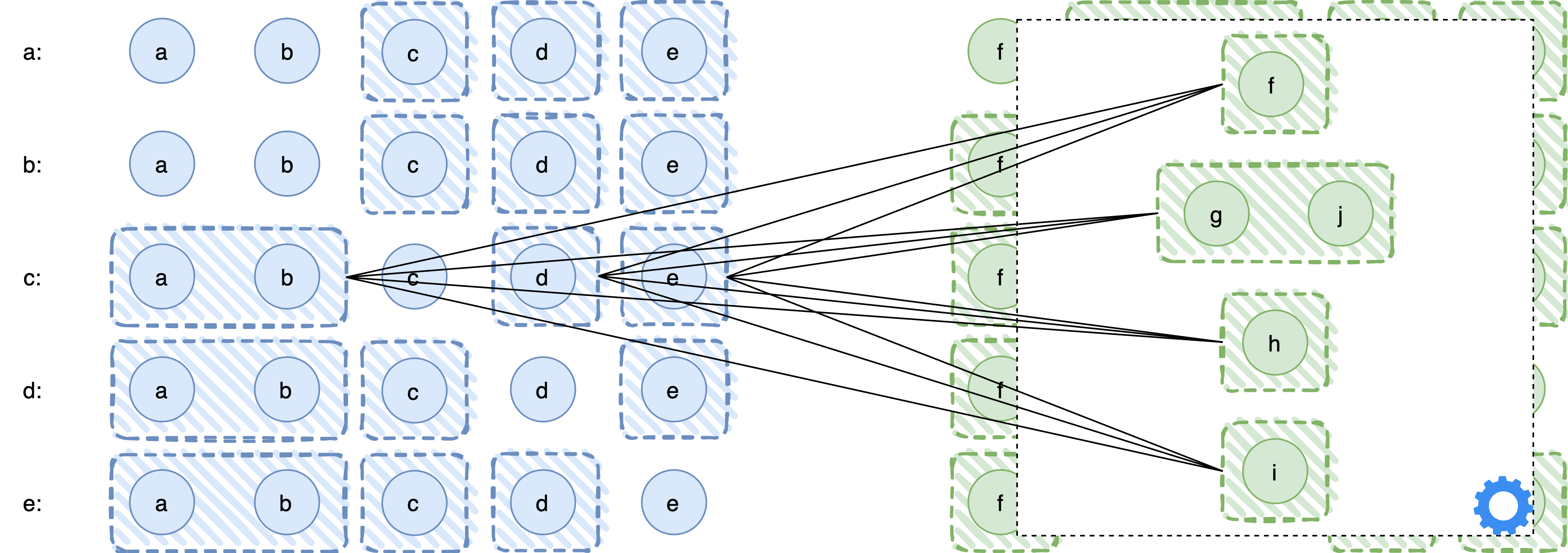
Let’s proceed again through an example. To keep the example simple, we now consider two disjoint sets of processes P1 = {a, b, c, d, e} and P2 = {f, g, h, i, j}. The fail-prone systems are shown in the following diagram. As before, processes are represented by circles and fail-prone sets are depicted by shaded, rectangular areas. For example, the fail-prone system of process a is Fa = { {c}, {d}, {e} }, for c it is Fc = { {a, b}, {d}, {e} }, and so on. (The horizontal order of processes in P2 is intentionally f, g, j, h, i because that lets us show the fail-prone set {g, j} as a contiguous area.)
Ideally, we would like to use our result from the symmetric case, the cartesian composition rule that considers also common processes. To do so, we would have to let each process in one system do the pairwise union between its fail-prone sets and the fail-prone sets of the other system. That would indeed work, but… what are the “fail-prone sets of the other system”? In the asymmetric model, each process has its own fail-prone sets, and no common notion of trust exists. If only we could come up with a notion that “summarizes” the trust assumptions of an ABQS into a single BQS…
The tolerated system of an ABQS
Recall that in asymmetric BQS, no common understanding of the world exists, either because there is not enough knowledge to assess the system, or because the participating processes simply do not agree with each other. On the contrary, every process expresses its own beliefs and expectations, and no global notion of “correct” belief exists. In every execution, however, there will be a ground truth, manifested by a set of actually faulty process, and not all members of the system will have correctly anticipated this ground truth. Again, since there is no global understanding of the world, this is expected to happen. However, the process might still be able to make progress (where progress is defined by the protocol they are running) if “enough” processes have correctly foreseen which others would fail or would make erroneous assumptions about those who would fail. These “enough many” processes can be formally defined: they are called a guild. Recent works on consensus with ABQS have conditioned safety and liveness properties on the existence of such a guild. In the context of Byzantine consensus, Cachin and Zanolini show that a guild is required to solve asynchronous consensus and that consensus properties are guaranteed in all executions with a guild.
The tolerated system captures this resilience of an ABQS. It contains those subsets of processes (called the tolerated sets) that are not necessary for the existence of a guild. The tolerated system characterizes the executions in which some of the processes in the ABQS will be able to operate correctly and make progress. In that sense, the tolerated system of an ABQS is the counterpart of the fail-prone system for a BQS. We show on our paper that the tolerated system an ABQS will always be a BQS (i.e., it will always satisfy the Q3-condition). It is a central concept for composing two ABQS because it allows external parties, or clients, to interact with an ABQS. Formally, the tolerated system is defined as follows.

Let’s try to calculate the tolerated system for the first asymmetric system in our example. In the simplest way, we have to check for every subset of P1 whether it is a tolerated set. We can start with the set {a}, and observe that, if it fails, processes c, d, and e are wise and they form a guild (actually, one has to formally define a guild to prove that {c, d, e} form one, but we will not be that detailed here). The same applies if {b} fails, in which case the guild is again {c, d, e}. Actually, we can even tolerate the failure of {a, b} (both processes fail in the same execution), again with {c, d, e} as a guild. Moreover, if any one of {c}, {d}, {e} fails, we can also show that the rest of the processes form a guild. Thus, the tolerated set is T1 = { {a,b}, {c}, {d}, {e} }. In the same way we can calculate the tolerated set of the second ABQS, which is T2 = { {f}, {g,j}, {h}, {i} }.
We can, thus, as external parties, interact with the two ABQS using their tolerated sets.
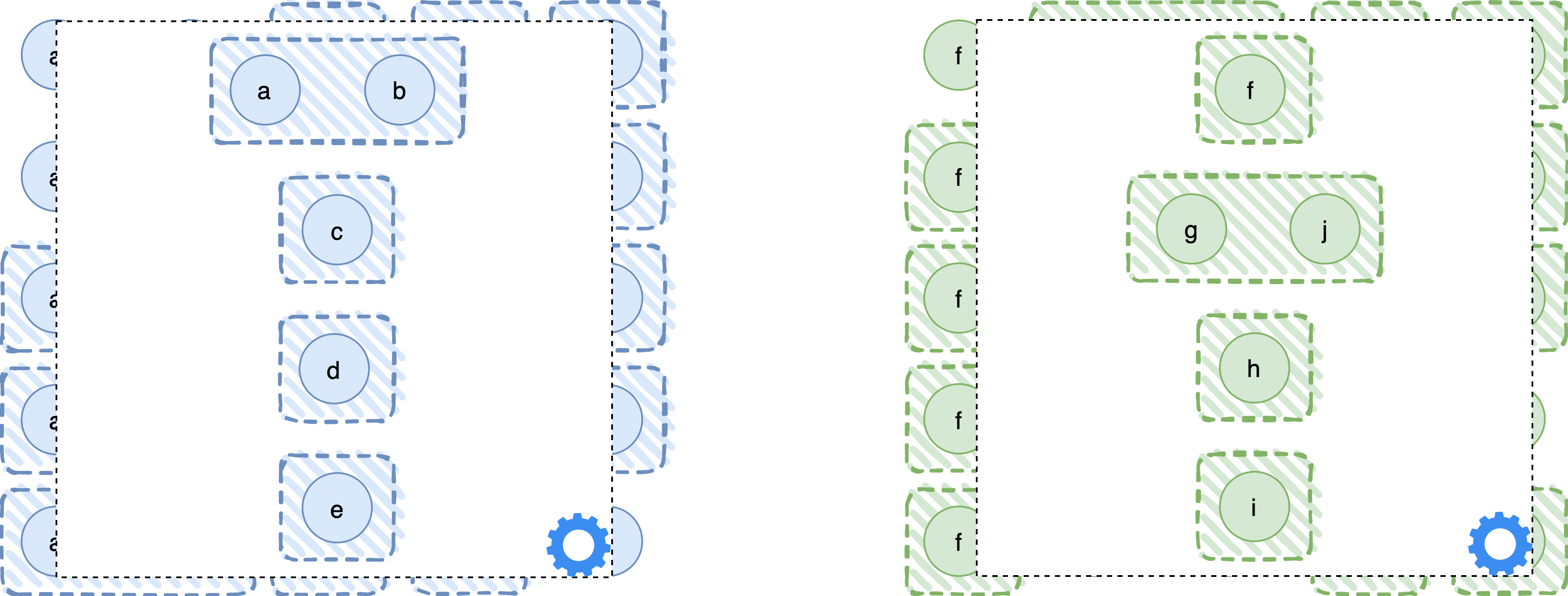
Applying the cartesian rule
We are now ready to perform the composition of our two ABQS. The idea is that every process in P1 uses the cartesian composition (with the special handling for common processes) between its fail-prone system and T2, and vice versa for processes in P2. In the next picture we show, for example, how process c would do the composition.
Technically, the rule is defined as follows.

The purification procedure
Finally, there is a subtle point we need to address. We have seen that the tolerated system of an ABQS will always satisfy the Q3-condition, and, by definition, the two ABQS will satisfy the B3-condition. However, it can be the case when P1 and P2 have common processes that the cartesian composition of an ABQS and a tolerated system does not satisfy the B3-condition. The good news, however, is that in such a case the “problematic” set, that is, the set that breaks the B3-condition, will not be a tolerated set (as a proof sketch, if it was a tolerated set then it would be in the tolerated system, and the tolerated system would not satisfy the Q3-condition). So, we can remove this “problematic” fail-prone set from the fail-prone system without sacrificing resilience, as it does not lead to a guild whatsoever.
This is formally captured by the purification procedure. Intuitively, it removes fail-prone sets that are “useless”, in the sense that they do not lead to the existence of a guild. Seen from a higher level, it is an expression of the fact that processes have their own beliefs, but also need to adapt to those of the others; a process might expect a set F to fail during an execution and construct its fail-prone system so as to be protected against F. However, if the beliefs of other processes are such that the failure of F does not lead to a guild, i.e., F is not tolerated, then the process can whatsoever not benefit from including F in its fail-prone system.
Composition in practice
In networks implementing consensus like this, the composition could be initiated by any process in P1, for example. This process sends a composition-request message to all members of P2, which in turn decide whether to accept the request or not, and reply accordingly with a composition-response message. Upon receiving the response, the processes in P1 also agree on whether to accept it and send an acknowledgement to P2. After this point, all processes can use the composite trust assumptions.
More details about our work and the complete description of our composition rules can be found in the research paper.
