Co-authored by Christian Cachin, Jovana Micic, Nathalie Steinhauer, and Luca Zanolini

A new, efficient protocol prevents attacks on decentralized finance platforms and ensures a novel notion of differential order-fairness for transactions in atomic broadcast.

Front-running attacks in decentralized finance

The nascent field of decentralized finance (or simply DeFi) suffers from insider attacks: Malicious miners in permissionless blockchain networks (like Ethereum) or Byzantine leaders in permissioned atomic broadcast protocols (like Tendermint Core used by the Cosmos Network) have the power of selecting messages carrying transactions that go into the ledger. They may also determine the final order of these transactions. On top, selfish participants may insert their own, fraudulent transactions before transactions of correct users. Both methods extract value from the network and harm its users. For instance, a decentralized exchange can be exploited by front-running, where a genuine message m carrying an exchange transaction is sandwiched between a message m^before and a message m^after. If m buys a particular asset, the insider acquires it as well using m^before and sells it again with m^after, typically at a higher price. Such front-running and other price-manipulation attacks represent a serious threat, and many practical blockchain networks, including Ethereum, are concerned about them. They are prohibited in traditional finance systems with centralized oversight but must be prevented technically in DeFi. The term miner extractable value (MEV) describes the profit that can be gained from such arbitrage opportunities.

Atomic broadcast and order fairness

The traditional properties of atomic broadcast, often somewhat imprecisely called consensus, guarantee a total order: that all correct parties obtain the same sequence of messages and that any message submitted to the network by a client is delivered in a reasonable lapse of time. However, these properties do not further constrain which order is chosen, and malicious parties in the protocol may therefore manipulate the order or insert their own messages to their benefit. Consequently, defining a property that guarantees a fair order in atomic broadcast has become an important task, especially in the Byzantine model. And new protocols that provide such a fairness property in an efficient way become absolutely essential.

Limitations of order fairness

Following work on order-fairness of Kelkar et al., we explore different notions of order fairness and identify some limitations that exist for imposing a fair order. Intuitively, order fairness aims at ensuring that messages received by “many” parties are scheduled and delivered earlier than messages received by “few” parties. The Condorcet paradox demonstrates, however, that such preference votes can lead to cycles, even if the individual votes of majorities are not circular.

Therefore, a fair order across all messages may not always exist. One possible solution is to output multiple messages together as a set (or batch), such that there is no order among them. The fair order is guaranteed only among the sets of messages.

Our models address asynchronous networks with n processes, of which f are faulty. Typically the number of faulty processes is bounded such that n > 3f. From results on differential validity of consensus by Fitzi and Garay, we have derived an important limitation on the achievable orderings. We consider the difference between how many correct processes prefer one of m and m’ over the other. If this value is too small, in particular, smaller than 2f, then no protocol exists to deliver them in fair order.

Differential order fairness

We introduce differential order fairness as a notion aligned with this impossibility and are convinced that it captures the benefits and the limitations of order-fair atomic broadcast adequately. It is quantified through an order-fairness parameter κ, with smaller values of κ ensuring stronger fairness properties. Intuitively, our notion means the following:

• When the number of correct processes that broadcast a message m before a message m’ exceeds the number that broadcast m’ before m by more than 2f + κ, for κ ≥ 0, then the protocol must not deliver m’ before m (but they may be delivered together).

Mathematically speaking, the properties of a differentially order-fair atomic broadcast protocol are:

We use of-broadcast and of-deliver for the events of broadcasting and receiving (and delivering to an application) a message in an order-fair manner. The value b(m, m’) denotes the number of correct processes that of-broadcast m before m’ in an execution. Here we assume that a correct process will of-broadcast m and m’ eventually and that, therefore, b(m, m’) + b(m’, m) = n − f.

Quick order-fair atomic broadcast

Our new protocol, called quick order-fair atomic broadcast, implements differential order fairness and is more efficient than existing algorithms.

The protocol operates in rounds, works with optimal resilience n > 3f, requires O(n^2) messages to deliver one payload on average, and needs O(n^2 L+n 3 λ) bits of communication, with payloads of up to L bits and cryptographic λ-bit signatures.

The first part of the protocol disseminates the locally observed orderings of the incoming payload messages among all processes. Every process maintains a log of the payloads as it has received and of-broadcast them. These logs are then sent around to all others, through multiple, so-called Byzantine consistent broadcasts. Finally, a common snapshot of these broadcasts is obtained using a validated Byzantine consensus primitive.

When the processes agree on the message logs for a specific round, we say that they have computed a cut. The message order is then determined in the second part of the protocol, which is entirely deterministic. In particular, the protocol starts to build a graph, where the vertices represent all new payloads from the message logs up to the cut. An edge (m, m’) indicates that m should at most be of-delivered before m’ (but never after m’). All payload messages with cyclic dependencies among them will be of-delivered together as a set. For deriving this information, the algorithm repeatedly detects all strongly connected components in the graph. Then it collapses the cycle to a single vertex, composed of multiple payload messages.

Note that cycles may also extend beyond the cut and the currently known message logs. To cope with this situation, we count in C[m] how many times a message m appears in the message logs up to the cut of the round. We require that any message m is only of-delivered in a round after it holds C[m] >= (n+f-κ)/2, which ensures that it may no longer become part of a cycle.

An example

We conclude by showing an example. Let us consider a system of n = 4 processes, of which three (p₁, p₂, and p₃) are correct and one (p₄) is faulty (f = 1). We fix the order-fairness parameter κ = 0. Every correct process of-broadcasts three messages m_a, m_b, and m_c, in an order that forms a Condorcet cycle. The Byzantine process p₄ does not of-broadcast. Suppose all messages are included in the cut c of round r at the correct processes. Moreover, consensus decides to consider the the messages up to c for round r.

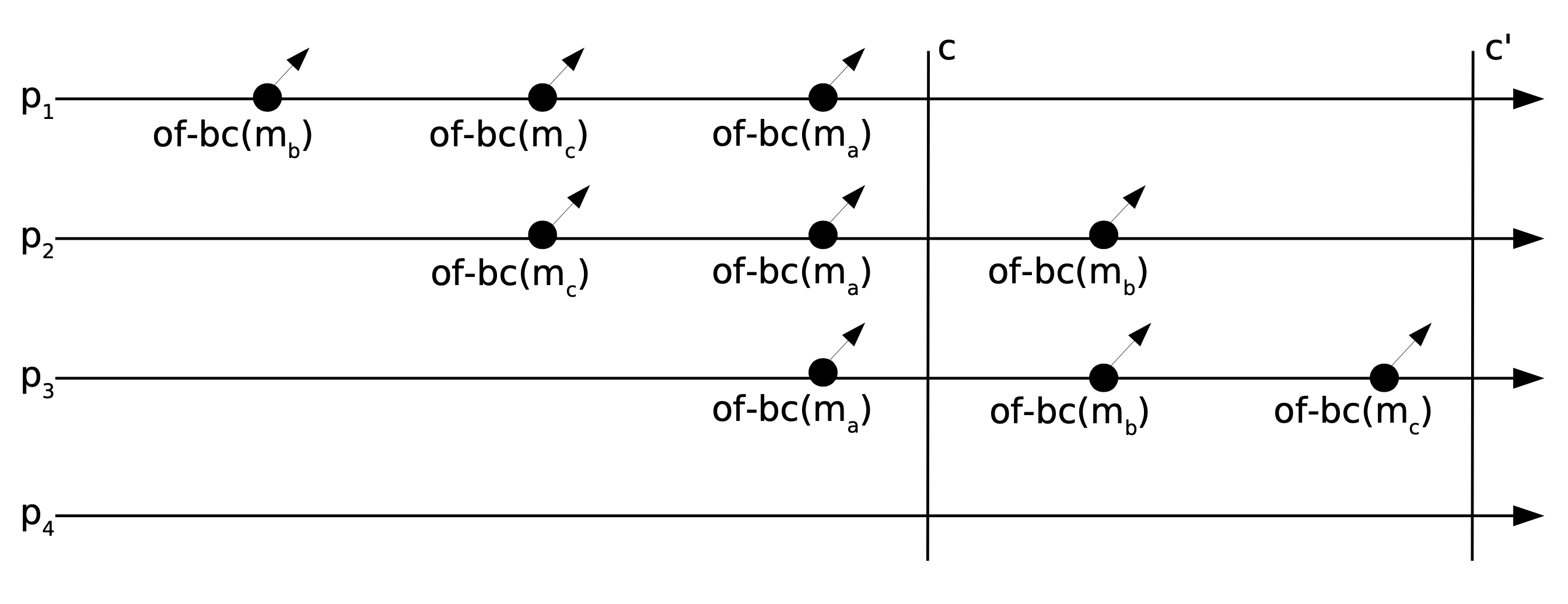
A matrix M is computed to count in an entry M[m][m’] how many message logs contain m before m’ up to the cut. The matrix for the example and the corresponding graph are:

Because C[m_b] = 1 < n/2, no payload message is of-delivered in this round. The protocol continues with another round r’ obtaining a cut c’. In this round, the matrix M and the graph become:

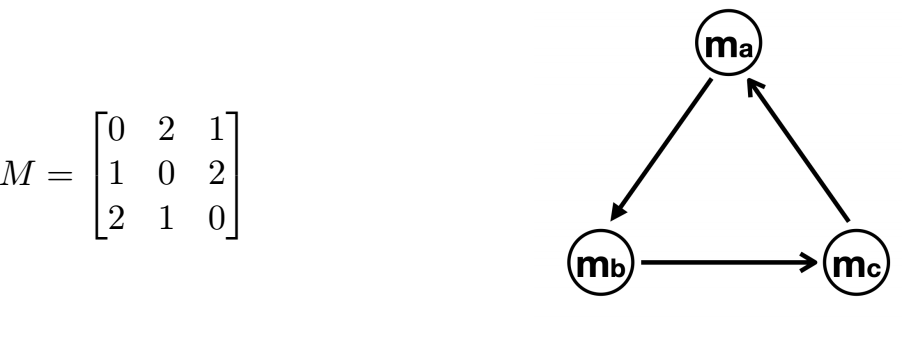
At this point, the protocol of-delivers {m_a, m_b, m_c} together, from a collapsed vertex, because now C[m_a] = C[m_b] = C[m_c] = 3 >= 2.5 = (n+f)/2.

Outlook

Whether fair ordering protocols will be deployed “on-chain” or “off-chain” remains to be seen - both solutions are possible. The leading blockchain oracle network Chainlink has already announced Fair Sequencing Services that will bring fair transaction-ordering protocols to Ethereum and other networks.

Our differential model and the quick order-fair atomic broadcast are presented at the Financial Cryptography and Data Security (FC) conference in May 2022 in Grenada. The paper will later appear in the proceedings. FC is the major international forum for computer-science research on financial security and privacy, especially when using cryptographic techniques. A strong focus is placed on advancements in blockchain technologies and cryptocurrencies.

A longer version of our research paper is available at https://arxiv.org/abs/2112.06615.